Il problema dell'interpolazione mediante il polinomio interpolatore di Lagrange consiste nel trovare una funzione che passi per tutti i punti nodali. Tuttavia è conveniente optare a volte una tecnica alternativa, in cui si procede nel modo seguente: Invece di trovare un unico polinomio di grado eleveto, che passi per tutti i punti nodali, si trovano piu' polinomi di grado inferiore sul generico sottointervallo di suddivisione. Questi polinomi prendono il nome di splines.
Splines
Consideriamo l'intervallo \([a, b]\) in cui vogliamo interpolare la nostra funzione oppure vogliamo cercare qualcosa che interpoli un insieme di punti nodali. Consideriamo i sottointervalli di \([a, b]\) che si ottengono considerando a due a due le proiezioni sull'asse \(x\) dei punti nodali: \([x_{j-1}, x_j]\) con \(j=1...n\).
una spline di grado \(k\) "\(S_k(x)\)" associata ai nodi in \([a, b]\) è una funzione ottenuta dall'unione di \(n\) polinomi tale per cui valgano le due condizioni: $$ \begin{cases} S_k(x) \in P_k \hspace{2cm} \forall x \in [x_{j-1}, x_j] \\ S_k(x) \in C^{[k-1]} \hspace{2cm} \forall x \in [a, b] \\ S_k(x_i) = y_i \end{cases} $$
In sostanza:
- In ogni sottointervallo, la spline deve essere un certo polinomio di grado \(k\).
- In tutto l'intervallo, la funzione deve essere derivabile al piu' \(k-1\) volte con derivata \(k-1\)-esima continua (condizione di allacciamento).
- Nei punti nodali, la spline è pari alla funzione di partenza (condizione di interpolazione).
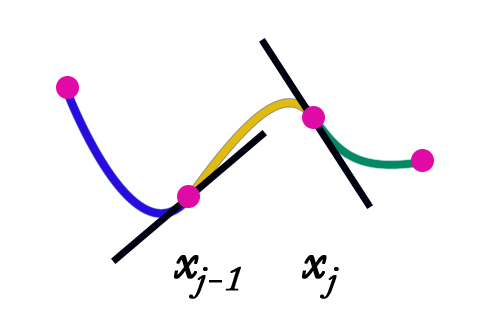
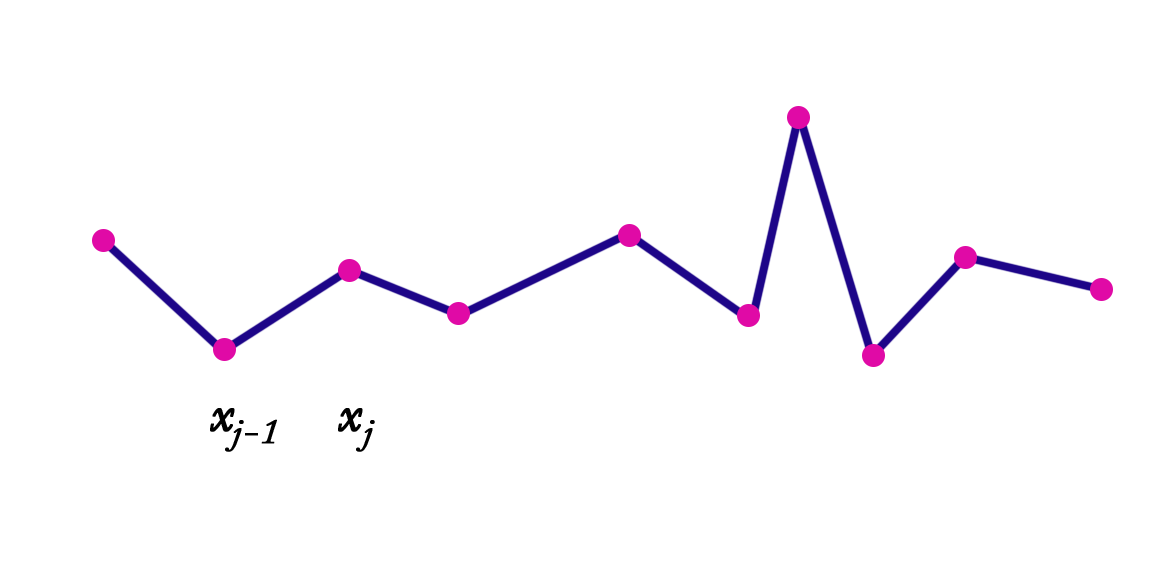
Per capire, ad esempio una spline di grado uno: \(S_1(x)\) in ciascun sottointervallo deve essere un polinomio di grado \(1\) "una retta", mentre vista globalmente in tutto \([a, b]\) deve essere una funzione di classe \(C^0\) "cioè continua". Questo vuol dire che può ammettere un insieme finito di punti angolosi in cui la derivata non esiste pur essendo continua come in figura a sinistra. In una spline di grado \(2\) in ciascun sottointervallo la funzione deve essere una parabola, mentre vista globalmente deve avere derivata prima continua. Cio significa che passando da un sottointervallo all'altro non vi devono essere spigoli. La spline di grado \(2\) o superiore deve avere delle condizioni di "allacciamento".
Splines Cubiche
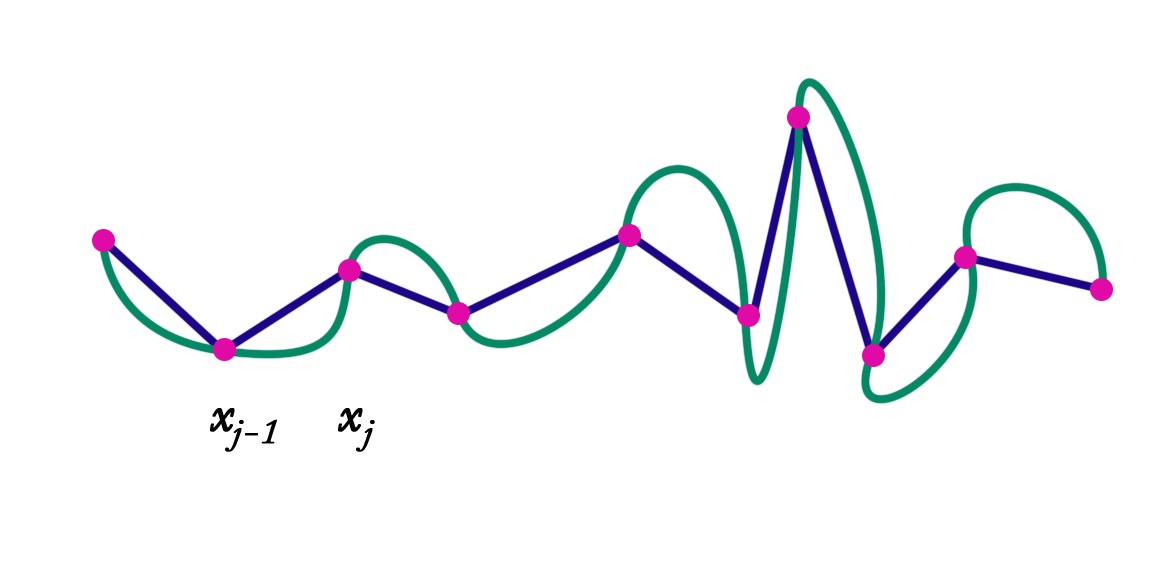
Le spline di secondo grado hanno derivata prima continua, ma derivata seconda discontinua. Per diversi problemi fisici è conveniente utilizzare splines cubiche che garantiscono la continuità fino alla derivata seconda su tutto l'intervallo. Una spline cubica è l'unione di \(n\) polinomi di grado \(3\) su ogni sottointervallo con condizioni di aggancio fino al terzo ordine. Si tratta di trovare \(n\) polinomi cubici: $$ S_{3j}(x) = Ax^3 + Bx^2 + Cx+D = 0 $$
Tale per cui si abbia che: in ciascun punto la spline sia pari al valore della funzione da interpolare, ed inoltre siano garantite le condizioni di aggancio sui nodi.