Il Nastro
Breve biografia di Mobius
August Ferdinand Moebius nasce il 1790 vicino Lipsia e Jena (Sassonia / Germania) in un'epoca di cambiamenti mentre Mozart componeva le sue opere a Vienna. Studiò a Lipsia era affascinato dalla matematica. Era un tipo introverso e timido, i Moebius discendono da una famiglia di studiosi, ingegneri e dotti. August Ferdinand aveva studiato in gioventu' astronomia teorica con Gauss a Gottinga che lo considerava il piu' dotato tra i suoi studenti(divenne direttore dell'osservatorio di Lipsia nel 1848) e famoso per la divulgazione astronomica, il nastro divenne noto solo dopo la sua morte. Lo scopri in un settembre del 1858 (anno in cui fu inventata la matita con la gomma) studiando le tassellazioni delle superfici Scarso professore, solitario attento e mitigoso con dedizione agli studi. Lavorò dal 1827 al 1831: Trigonometria, Astronomia, Geometria proiettiva, trasformazioni. La sua Tesi sull'occultazione stelle fisse è del 1815.

Proprietà
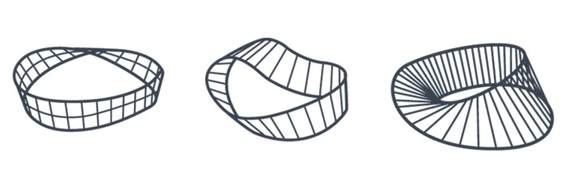
E una superficie non orientabile
Sezionamento: se tagliamo un NdM lungo il centro si ottiene un unico anello chiuso (con 2 mezze torsioni) invece che due.
BSezionamento: se tagliamo nuovamente questa striscia lungo la metà otteniamo due nastri intrecciati.
3Sezionamento: se tagliamo lungo un terzo al margine un NdM otteniamo due anelli intrecciati (un nastro stretto di Moubius ed una nastro con due mezze torsioni quello piu largo).
Qualsiasi striscia con un numero dispari di mezze torsioni --> Simil Nastro di Mobius.
Qualsiasi striscia con un numero pari di mezze torsioni --> Simil Cilindro
Se facciamo \(m\) torsioni (\(m \pi [rad] \)) prima di incollare la striscia:
\(m\) pari: Creiamo una superficie con 2 facce e 2 bordi -> se la striscia e tagliata al centro otteniamo due anelli ciascuno con m mezze torsioni (legate \({1\over 2m}\) volte). \(m\) dispari: Creiamo una superficie con una sola faccia e un solo bordo -> se la striscia e tagliata al centro. otteniamo un solo anello con \(2m+2\) mezze torsioni e se \(m>1\) annodato
Equazioni parametriche del Nastro di Mobius
Una classica parametrizzazione del Nastro in \( \mathbb R^3 \) in coordinate cartesiane è la seguente (dove \( 0 \leq u < 2\pi \) e \(-1 \leq v \leq 1 \)): $$ x(u, v) = \left(1+{v \over 2}cos{u \over 2}\right)cos(u) $$ $$ y(u, v) = \left(1+{v \over 2}cos{u \over 2}\right)sin(u) $$ $$ z(u, v) = \left({v \over 2}sin{u \over 2}\right)$$
Un sandwitch di Mobius
Due striscie una sull'altra con mezza torsione. Si sonda con uno stuzzicadenti che tra di esse c'e spazio vuoto si prova a colorare una delle due ma sembra essere unica, si separano e si scopre di avere una sola striscia con 4 mezze torsioni.
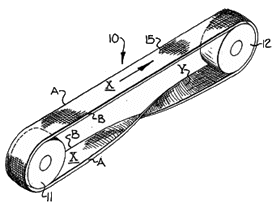
Brevetti e diavolerie Moebiussiane
Un nastro di Moebius è un affascinante superficie con una sola faccia ed un solo bordo. Per ottenere un nastro
di questo tipo è sufficiente unire le due estremità di una lunga striscia di carta dopo aver fatto fare ad una delle due estremi di esse una
torsione di 180* rispetto all'altra. Il risultato è una superficie con una sola faccia su cui un insetto può spostarsi da un punto qualsiasi ad un altro senza mai attraversare un margine;
viceversa se si uniscono le due terminazioni senza fare torsioni si ottiene un semplice cilindro o anello. E' forse un oggetto che riesce a carpire alcune proprietà misteriose dello spazio.

Breve biografia di Mobius
August Ferdinand Moebius nasce il 1790 vicino Lipsia e Jena (Sassonia / Germania) in un'epoca di cambiamenti mentre Mozart componeva le sue opere a Vienna. Studiò a Lipsia era affascinato dalla matematica. Era un tipo introverso e timido, i Moebius discendono da una famiglia di studiosi, ingegneri e dotti. August Ferdinand aveva studiato in gioventu' astronomia teorica con Gauss a Gottinga che lo considerava il piu' dotato tra i suoi studenti(divenne direttore dell'osservatorio di Lipsia nel 1848) e famoso per la divulgazione astronomica, il nastro divenne noto solo dopo la sua morte. Lo scopri in un settembre del 1858 (anno in cui fu inventata la matita con la gomma) studiando le tassellazioni delle superfici Scarso professore, solitario attento e mitigoso con dedizione agli studi. Lavorò dal 1827 al 1831: Trigonometria, Astronomia, Geometria proiettiva, trasformazioni. La sua Tesi sull'occultazione stelle fisse è del 1815.

Proprietà
E una superficie non orientabile
Sezionamento: se tagliamo un NdM lungo il centro si ottiene un unico anello chiuso (con 2 mezze torsioni) invece che due.
BSezionamento: se tagliamo nuovamente questa striscia lungo la metà otteniamo due nastri intrecciati.
3Sezionamento: se tagliamo lungo un terzo al margine un NdM otteniamo due anelli intrecciati (un nastro stretto di Moubius ed una nastro con due mezze torsioni quello piu largo).
Qualsiasi striscia con un numero dispari di mezze torsioni --> Simil Nastro di Mobius.
Qualsiasi striscia con un numero pari di mezze torsioni --> Simil Cilindro
Se facciamo \(m\) torsioni (\(m \pi [rad] \)) prima di incollare la striscia:
\(m\) pari: Creiamo una superficie con 2 facce e 2 bordi -> se la striscia e tagliata al centro otteniamo due anelli ciascuno con m mezze torsioni (legate \({1\over 2m}\) volte). \(m\) dispari: Creiamo una superficie con una sola faccia e un solo bordo -> se la striscia e tagliata al centro. otteniamo un solo anello con \(2m+2\) mezze torsioni e se \(m>1\) annodato
Equazioni parametriche del Nastro di Mobius
Una classica parametrizzazione del Nastro in \( \mathbb R^3 \) in coordinate cartesiane è la seguente (dove \( 0 \leq u < 2\pi \) e \(-1 \leq v \leq 1 \)): $$ x(u, v) = \left(1+{v \over 2}cos{u \over 2}\right)cos(u) $$ $$ y(u, v) = \left(1+{v \over 2}cos{u \over 2}\right)sin(u) $$ $$ z(u, v) = \left({v \over 2}sin{u \over 2}\right)$$
Un sandwitch di Mobius
Due striscie una sull'altra con mezza torsione. Si sonda con uno stuzzicadenti che tra di esse c'e spazio vuoto si prova a colorare una delle due ma sembra essere unica, si separano e si scopre di avere una sola striscia con 4 mezze torsioni.

Brevetti e diavolerie Moebiussiane
- Antenna Lemniscata
- Nastri trasportatori, magnetici che durano il doppio e sono piu corti.
- Componenti elettronici
- Rompicapo, sega a nastro
- ecc
