Il sistema trigonometrico - Giuseppe Sottile

Il sistema trigonometrico:

$$ c_0 = {1 \over \sqrt{2\pi}} \hspace{1cm} c_n = {cos(nx)\over \sqrt{\pi}} \hspace{1cm} s_n = {sin(nx) \over \sqrt{\pi}}$$

E' un sistema di vettori (monomi) trigonometrici ortonormale. Si dimostra che esso costituisce una base di uno spazio vettoriale di Hilbert (*per dimostrare che si tratta di una base, bisogna mostrare che l'unico vettore ortogonale a tutti i vettori del sistema trigonometrico è il vettore nullo)

Detto in altre parole: una qualunque funzione continua ortogonale a tutti i vettori del sistema trigonometrico è la funzione nulla. Supponiamo senza perdita di generalità di lavorare nell'intervallo $[-\pi, \pi]$, cioè: $$ f:[-\pi, \pi] \rightarrow \mathbb C $$ Supponiamo anche che: $ \langle c_0, f\rangle = \langle c_n, f\rangle = \langle s_n, f\rangle = 0$.
Allora $ f = 0$.

Anzitutto, possiamo concentrarci a lavorare con una funzione reale. Perchè se fosse complessa avremo che: $\small f(x) = Ref(x) + iImf(x) $. Inoltre $\small \langle c_0, f\rangle = 0 $ implicherebbe che $ \small \langle c_0, Ref(x) + iImf(x)\rangle = \langle c_0, Ref(x) \rangle + i\langle c_0, Imf(x)\rangle = 0$, il che è lo stesso che dire: $ \small \langle c_0, Ref(x) \rangle = 0 $ e $ \small \langle c_0, Imf(x) \rangle = 0 $, (Si ricondurrebbe tutto a funzioni reali!

$$ \diamond $$

$ DIM: $ (reduction ad absurdum)

Supponiamo per ipotesi di prendere una funzione continua reale $ f $ tale per cui essa è ortogonale a tutti i vettori del sistema trigonometrico, (ma $f \neq 0$).
Questo implicherebbe che esiste un certo $x_0 \in [-\pi, \pi]$ tale che $ f(x_0) \neq 0$, supponiamo che sia $f(x_0) > 0 = \eta$.

Siccome la funzione è continua allora: $ f(x_0) = \lim_{x\to x_0}f(x) $

Inoltre vale il teorema della permanenza del segno: Se $ f(x) = \eta $: per ogni $ \epsilon > 0 $ esiste un $ \delta > 0 $ tale che: $ |\eta - f(x)|<\epsilon $ per ogni $ x \in (x_0-\delta, x_0+\delta) $. Ossia che $ -\epsilon < f(x)-\eta < \epsilon $ il che vuol dire: $ f(x) > \eta - \epsilon $. Se prendiamo $ 0 < \epsilon < {\eta \over 2} $ avremo: $ f(x)>{\eta \over 2} $ per ogni $ \small x \in (x_0-\delta, x_0+\delta) $.

Costruiamo ora il seguente polinomio trigonometrico (combinazione lineare di monomi trigonometrici): $$ t(x) = 1-cos\delta + cos(x-x_0) = \begin{cases} > 1, |x-x_0|<\delta \\ < 1, |x-x_0|>\delta \\ =1, |x-x_0| = \delta \end{cases} $$

Es: plot([1 - cos(0.1) + cos(x - 0.5), 1], x = -0.3 .. 0.8)

Lo stesso accade se eleviamo il polinomio ad una certa potenza positiva: $T_n(x) = [t(x)]^n $:

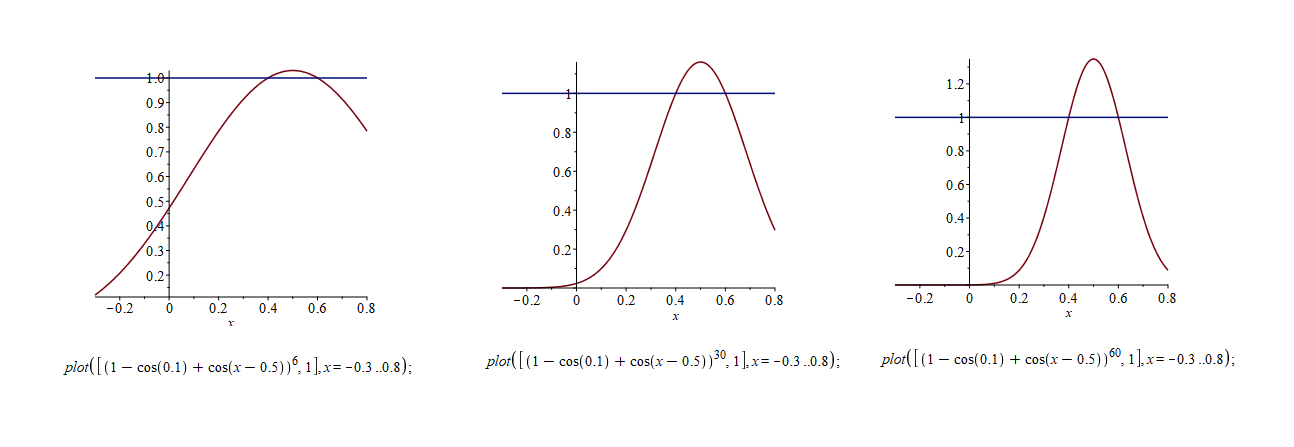
poniamo ora $\mu = min|t(x)|$ quando $ |x-x_0|<{\delta \over 2} $ il che è lo stesso che dire: $ x \in (x_0-{\delta \over 2}, x_0 + {\delta \over 2}) $. Siccome naturalmente in questo intervallo $t(x)>1$ lo sarà anche $\mu = min|t(x)| > 1$

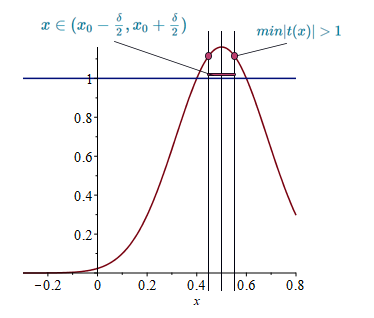
Vale questa relazione in $|x-x_0|<{\delta \over 2}$: $$\mu_n = min(T_n(x)) \geq \left( min(t(x))\right)^n = \mu^n $$ $$ \mu_n \geq \mu^n $$
Ora mettiamo insieme questo ragionamento con l'ipotesi vera che la nostra $f$ continua sia ortogonale a tutte le funzioni del sistema (in particolare ad una loro combinazione lineare ovvero al polinomio $T_n$ per ogni $n=1, 2,...$. $$ \langle T_n, f\rangle = 0 $$ $$ = \int_{-\pi}^{\pi} T_n(x)f(x)dx =$$ $$ = \int_{-\pi}^{x_0 - \delta} T_n(x)f(x)dx +\int_{x_0 - \delta}^{x_0 + \delta} T_n(x)f(x)dx +\int_{x_0 + \delta}^{\pi} T_n(x)f(x)dx = 0$$ $$ \Downarrow $$ $$ \int_{x_0 - \delta}^{x_0 + \delta} T_n(x)f(x)dx = - \int_{-\pi}^{x_0 - \delta} T_n(x)f(x)dx - \int_{x_0 + \delta}^{\pi} T_n(x)f(x)dx $$ Chiaramente l'integrale $ \int_{x_0 - \delta}^{x_0 + \delta} T_n(x)f(x)dx $ è certamente una quantità positiva essendo svolto su un tratto di funzione $ > 1 $, quindi posso scrivere: $$ 0 \leq \int_{x_0 - \delta}^{x_0 + \delta} T_n(x)f(x)dx = \left| \int_{-\pi}^{x_0 - \delta} T_n(x)f(x)dx + \int_{x_0 + \delta}^{\pi} T_n(x)f(x)dx \right| \leq $$ $$ \leq \left| \int_{-\pi}^{x_0 - \delta} T_n(x)f(x)dx \right| + \left| \int_{x_0 + \delta}^{\pi} T_n(x)f(x)dx \right| \leq $$ $$ \leq \int_{-\pi}^{x_0 - \delta} \left|T_n(x)f(x) \right| dx + \int_{x_0 + \delta}^{\pi} \left| T_n(x)f(x) \right| dx \leq $$ La funzione $T_n(x)$ sappiamo che nell'intervallo ($-\pi, x_0 - \delta$) e ($x_0 + \delta, \pi$) è costantemente minore di $1$, quindi la quantità di sopra è maggiorata da: $$ \leq \int_{-\pi}^{x_0 - \delta} \left|T_n(x)f(x) \right| dx + \int_{x_0 + \delta}^{\pi} \left| T_n(x)f(x) \right| dx \leq \int_{-\pi}^{x_0 - \delta} \left|f(x) \right| dx + \int_{x_0 + \delta}^{\pi} \left|f(x) \right| dx \leq $$ $$ \leq \int_{-\pi}^{x_0 - \delta} \left|f(x) \right| dx + \int_{x_0 + \delta}^{\pi} \left|f(x) \right| dx + \int_{x_0 - \delta}^{x_0 + \delta} \left|f(x) \right| dx \leq $$ $$ \leq \int_{-\pi}^{\pi} \left|f(x) \right| dx < \infty $$ Siccome la $f$ è continua, lo sarà anche il suo modulo e quindi l'integrale sara finito.
In sostanza abbiamo scoperto che (ricordando che: $\mu_n \geq \mu^n$ e che $ f(x)>{\eta \over 2} $ ): $$ 0 \leq \int_{x_0 - \delta}^{x_0 + \delta} T_n(x)f(x)dx < \infty $$ Siccome l'integrale è un valore positivo avremo che: $$ \int_{x_0 - \delta}^{x_0 + \delta} T_n(x)f(x)dx \geq \int_{x_0 - {\delta\over 2}}^{x_0 + {\delta\over 2}} T_n(x)f(x)dx \geq {\mu^n \eta \over 2 }\delta $$ Riassumendo: $$ {\mu^n \eta \over 2 }\delta \leq \int_{x_0 - \delta}^{x_0 + \delta} T_n(x)f(x)dx < \infty $$ Ma siccome $ \mu > 1 $ allora $ \lim_{n\to\infty} {\mu^n \eta \over 2 }\delta = \infty $. Ecco trovato l'assurdo! (La funzione deve per forza essere identicamente zero). $$ \infty \leq \int_{x_0 - \delta}^{x_0 + \delta} T_n(x)f(x)dx < \infty $$ $$ \square $$