Un numero complesso \( z \) nella sua forma più generale e semplice, si può esprimere come la somma di un numero reale puro \( x \) e di un numero immaginario \( iy \), che come visto, sarebbe il prodotto di un numero reale puro \( y \) con un oggetto speciale, che i matematici usano indicare con \( {\large i} \) ^[1] e che si chiama unità immaginaria. $$ {\Large z = x + iy } $$

Dove \( x \) e \( y \) sono due numeri reali \( x \in {\mathbb R}, y \in {\mathbb R} \), ed inoltre \( \sqrt{-1} = i \)

Ricapitolando in termini matematici possiamo esprimere l'insieme dei numeri complessi più propriamente come:

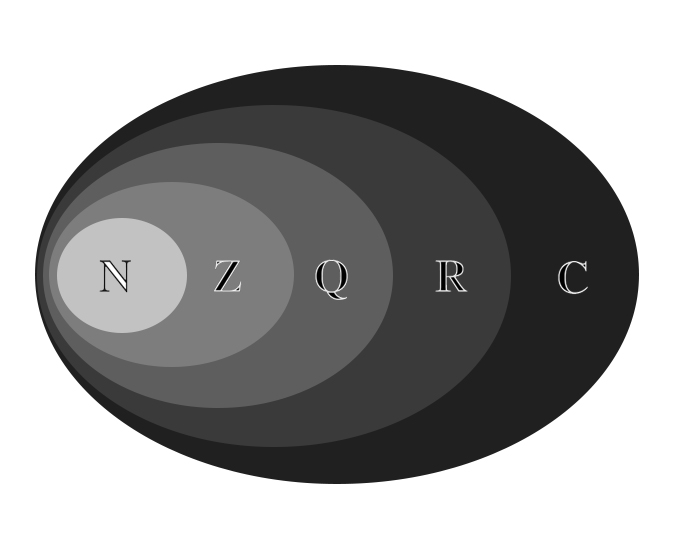
$$ {\mathbb C} = \left\{ z = (x, y) \hspace{1mm}|\hspace{1mm} x \in {\mathbb R}, y \in {\mathbb R} \wedge \sqrt{-1} = i \right\} $$

Secondo la rapprsentazione insiemistica di Eulero-Venn i numeri complessi costituiscono un ampliamento dei numeri reali: $$ {\large \mathbb N \subseteq \mathbb Z \subseteq \mathbb Q \subseteq \mathbb R \subseteq \mathbb C } $$