Consideriamo due numeri complessi \( z_1 \) e \( z_2 \). Esprimiamoli mettendo in evidenza parte reale e parte immaginaria: $$ z_1 = a + ib \hspace{3cm} z_2 = c + id $$

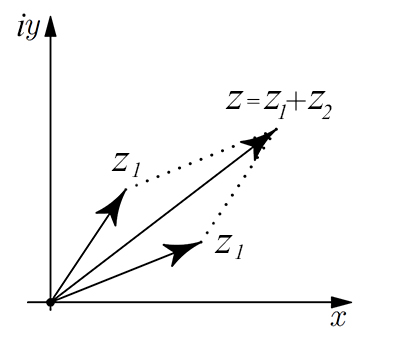
Per sommare due numeri complessi si sommano semplicemente le parti reali e le parti immaginarie separatamente. Il complesso risultante sarà costituito da una parte reale(somma delle parti reali) e da una parte immaginaria(somma delle parti immaginarie) $$ z_1 + z_2 = z = (a+c) + i(b+d) $$ $$ Re\{z\} = a+b \\ Im\{z\} = c+d $$ Riportando sul piano complesso i numeri \(z_1\) e \(z_2\) la somma è rappresentata dalla regola del parallelogramma. Ciò ci fà intuire che i numeri complessi hanno un comportamento molto simile a quello dei vettori di \( {\mathbb R^2} \), dove le componenti corrispondono alla parte reale ed immaginaria.